動的計画法解説 [SRM 468 Div2 250/Div1 500]
目次
王様は長い間出張していたので、できるだけ早く女王のもとに帰りたいと思っています。王様は都市 0 におり、女王は都市 N (1 <= N <= 50)に居ます。全ての都市 i (0 <= i <= N - 1) に対して陸路と空路があります。配列 roadTime, flightTime が与えられ、それぞれの i 番目の要素は都市 i から都市 i + 1 までの陸路、空路の所要時間 (1 以上 1000 以下) を表わします。しかし王国の科学力は低く、空路による移動は墜落の危険を伴います。そのため、王女は王様に空路は K (0 <= K <= N) 回までに留めるように言いました。王様が王女に会うための最短時間を求めなさい。
出題元 SRM 468 Div2 250
 | 黒井先生からこんな宿題が出ていたわ。 |
 | って言うかさあ。 |
 | 何よ。 |
 | 全部空路で行けば良くね? |
 | まあ、最初はそう思うわね。でもサンプルを見ると空路の方が時間が掛かるケースもあるから特に空路<陸路という条件は無いみたいよ。 |
 | でも常識で考えておかしいよね。 |
 | あーもー空路がト○ロで陸路がネ○バスなんじゃないの? |
 | おお、なるほど。 |
 | 納得するのか。。。まあいいわ。問題に取り掛かりましょう。 |
 | とりあえずどっから取り掛かったら良いかわかんないな。 |
 | 難しい問題を解く場合は簡単な問題に変えてみるという手が有効よ。例えば K の制限を無くしてみたらどう? |
 | それなら簡単。ビットが立っている場合を空路とみなして全探索で書くとこんな感じかな。 |
public int minTime(int N, int[] roadTime, int[] flightTime, int K) {
int sum, min = Integer.MAX_VALUE;
for (int i = 0; i < (1 << N); i++) {
sum = 0;
for (int j = 0; j < N; j++) {
if ((i & (1 << j)) != 0) {
sum += flightTime[j];
} else {
sum += roadTime[j];
}
}
if (min > sum)
min = sum;
}
return min;
}
 | そうね。これに K の制限を加えるとどうなる? |
 | 空路が K 回までってことはビットの数が K 以下ってことだから、こうかな? |
public int minTime(int N, int[] roadTime, int[] flightTime, int K) {
int sum, min = Integer.MAX_VALUE;
for (int i = 0; i < (1 << N); i++) {
if (bitCount(i) > K)
continue;
sum = 0;
for (int j = 0; j < N; j++) {
if ((i & (1 << j)) != 0) {
sum += flightTime[j];
} else {
sum += roadTime[j];
}
}
if (min > sum)
min = sum;
}
return min;
}
private int bitCount(int val) {
int ret = 0;
for (int i = 0; i < 32; i++) {
if ((val & (1 << i)) != 0) {
ret++;
}
}
return ret;
}
 | まあそんなとこね。 |
 | よし!サンプル通った!あ、でも System test で TLE (*1) する。。。 |
(*1) TLE: 時間超過 (Time Limit Exceeded) の略。 TopCoder においては 2 秒以内にプログラムが終了しなければならない。
 | 外側の i のループは N = 50 の場合は何回周るのよ? |
 | 2^50 だから 1000 兆回以上か。そりゃ TLE するわな。かがみん先生!もう何も思い付きません! |
 | じゃあヒント。再帰を使って書いてみるのよ。 |
 | 再帰苦手なんだよね。。。書いてる途中であれ?あれ?ってなるし。 |
 | いきなり再帰のプログラムを書こうとすると途中で混乱することが多いわね。そんな時は漸化式を書いて、それを元にプログラムを書くと良いわよ。 |
 | ざんかしき? |
 | 「ぜんかしき」よ。例えば等差数列を表わすときに使う a[i] = a[i - 1] + 2 のようなやつよ。 |
 | それと再帰とどう関係があるの? |
 | 漸化式をプログラムで表現する場合に、再帰を使うと自然に表現できるのよ。 |
 | さっきの a[i] = a[i - 1] + 2 も表現できるの? |
 | できるわよ。最初だから例を見せるわ。 a[0] = 1, a[i] = a[i - 1] + 2 の例よ。 |
public int rec(int N) {
if (N == 0)
return 1;
return rec(N - 1) + 2;
}
 | 確かに漸化式の通りだ。今まで再帰のプログラムを見て、そのまま理解しようとしてわけわかんなくなってたけど、漸化式を見てから読むとすぐに理解できるね。 |
 | そ、そう。良かったわね。 |
 | 何か目覚めた!何か覚醒した!私にも見える!こ、これが俺の力? |
 | じゃ、じゃあ K の制限なしの場合の問題をやってみて。 |
 | うあああ、わからない。 |
 | 順番に行くわよ。漸化式を作るためには「添字」と「値」の両方が必要なの。 |
 | どういうこと? |
 | 例えばさっきの a[n] の例だと、添字である n を決めれば値が決まるわよね。 |
 | それ当たり前なんじゃないの? |
 | そうだけど!問題に応じて何を「添字」にして何を「値」にするのかを選択する必要があるってことよ。条件に応じて選択を変える場合もあるの。この問題の場合はそれぞれ何を使えば良いと思う? |
 | まず最短時間を求める問題だから「値」の方は最短時間で良いと思う。あと添字はそれぞれの都市を表わす i かな? |
 | それで漸化式を立ててみて。 |
 | うう。まだできない。 |
 | そういう時は具体的にやってみるの。 roadTime = {1, 2, 6}, flightTime = {4, 3, 5} の場合を考えてみて。漸化式は b[i] として。 |
 | b[i] は都市 i - 1 から i までの最短時間てことだね。まず i = 0 の場合は、まだどこにも行ってないから b[0] = 0 。 i = 1 の場合は陸路だと 1 、空路だと 4 かかるから b[1] = 1。 i = 2 の場合は陸路で b[2] = 2。 i = 3 の場合は空路で b[3] = 5。 |
 | そう来たか。。。その方法だとそれぞれの区間ごとに最短時間が求まるけど、最終的に求めたいものは何だっけ? |
 | 全部の合計。あ、だから b[0] から b[n] まで足したものが答えだね。 |
 | そうなんだが。例えばさっきの数列の例だと a[n] を計算しさえすれば a[0] から a[n] まで足さなくても答えを表わしていたよね。 b[i] もそんなふうに書けないかな。 |
 | つまり b[i] は都市を i 個通った時点の合計最短時間てことだね。 b[0] = 0, b[1] = 1 + b[0] = 1, b[2] = 2 + b[1] = 3, b[3] = 5 + b[2] = 8。 |
 | そうね。漸化式で表わすとどうなる? |
 | えっと b[i] = (都市 i - 1 から都市 i への陸路と空路のうち短い方) + b[i - 1]。 |
 | 日本語の部分を書き直すと? |
 | b[0] = 0, b[i] = min(roadTime[i - 1], flightTime[i - 1]) + b[i - 1] (i > 0) |
 | これで漸化式はできたわね。プログラムに書き直して。 |
 | できた!漸化式を見ながらだと再帰を書くとき混乱しなくて済むね。 |
private int[] r, f;
public int minTime(int N, int[] roadTime, int[] flightTime, int K) {
r = roadTime;
f = flightTime;
return b(N);
}
private int b(int i) {
if (i == 0)
return 0;
return Math.min(b(i - 1) + r[i - 1], b(i - 1) + f[i - 1]);
}
 | いやー長かった。ようやく終わったよ。 |
 | まだ続くけどね。ちょっと休憩しましょう。 |
~~休憩中~~
 | 再開するわよ。 |
 | 思ったんだけどさ。 |
 | 何よ。 |
 | 王様は女王に早く会いたいと思ってるかもしんないけど女王はぶっちゃけ会いたくないんじゃね?だから空路は K 以下にしろとか言ってるんじゃね? |
 | 問題批判はもういいから。さっきは K の制限を無くしていたけど今度は制限ありの場合の漸化式を書いてみて。 |
 | えーと、 K が入るんだよね。漸化式にできるのかな。 |
 | ヒントは b[i] の形ではなく b[i, j] の形よ。 |
 | i は都市の添字で b[i, j] 自体は合計最短経路というのは変わらないと思う。だから j で K を表わすのかな。 |
 | i 個の都市を通った後で j 回の空路が残っている場合の合計最短経路を b[i, j] とおいたら良いんじゃないかな。 |
 | それでやってみて。 |
 | j = 0 の場合は空路が無いから b[i, j] = b[i - 1, j] + r[i - 1] だね。それから i = 0 の場合はどこにも行ってないから b[i, j] = 0 だね。 |
 | そうね。 |
 | さっきの K 無しの場合と違って空路を使うと j が一つ減るから b[i, j] = min(b[i - 1, j] + roadTime[i - 1], b[i - 1, j - 1] + flightTime[i - 1]) (j > 0) だね。 |
 | 漸化式は完成ね。プログラムにして。 |
private int[] r, f;
public int minTime(int N, int[] roadTime, int[] flightTime, int K) {
r = roadTime;
f = flightTime;
return b(N, K);
}
private int b(int i, int j) {
if (i == 0)
return 0;
int road = b(i - 1, j) + r[i - 1];
if (j > 0)
return Math.min(road, b(i - 1, j - 1) + f[i - 1]);
else
return road;
}
 | よし!サンプル通った!あ、でもまた TLE。 |
 | そうね O(2^N) なのは変わらないからね。 |
 | じゃあなぜやらせた。 |
 | 次の準備のためよ。なぜ TLE するか説明するために roadTime = {1, 2, 6}, flightTime = {4, 3, 5}, K = 2 の場合を図にしてみましょう。 |
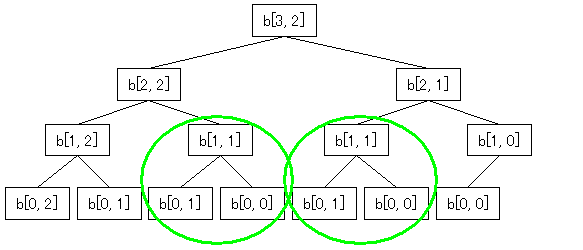
 | b[1, 1] の場合を2回計算してるね。 |
 | そうね。条件より 0 <= i, j <= 50 だから b[i, j] は多くとも 2500 通りしかないの。それなのに時間が掛かってしまうのは無駄な計算をたくさんやっているからよ。 |
 | 無駄をなくせば TLE しなくなる? |
 | そうよ。無駄をなくすために、既に計算済みのものは配列に格納しておくように変えてみましょう。これを「メモ化再帰」と言うわ。 |
 | できた。 |
private int[] r, f;
private int memo[][];
public int minTime(int N, int[] roadTime, int[] flightTime, int K) {
r = roadTime;
f = flightTime;
memo = new int[N + 1][K + 1];
for (int i = 0; i <= N; i++)
for (int j = 0; j <= K; j++)
memo[i][j] = -1;
return b(N, K);
}
private int b(int i, int j) {
if (memo[i][j] != -1)
return memo[i][j];
if (i == 0) {
memo[i][j] = 0;
} else {
int road = b(i - 1, j) + r[i - 1];
if (j > 0)
memo[i][j] = Math.min(road, b(i - 1, j - 1) + f[i - 1]);
else
memo[i][j] = road;
}
return memo[i][j];
}
 | 早いわね。 |
 | こーゆーのは得意。あ、 TLE しなくなった。全部通ったー!今度こそ終わりだね! |
 | ここまでは全て準備。 |
 | ぐっ。 |
 | さあいよいよ本題の動的計画法の説明に入るわよ。 |
 | で、でもさっきテスト通ったから黒井先生からの宿題は終わったんじゃ。 |
 | 動的計画法を使えってホームルームで言ってたわよ。 |
 | そ、そんな宿題を出す高校なんてないよね。。。 |
 | つべこべ言わず行くわよ。 |
 | ほーい。 |
 | 動的計画法を一言で言うと、さっきのメモ化再帰で使ったメモを直接求めてしまう方法よ。ちなみにメモ化再帰のことも動的計画法って呼ぶ場合があるわ。 |
 | じゃあ終わりでいいじゃん。 |
 | 黙れ。さっきの配列 memo[i][j] には何が入ってる? |
 | b[i, j] と同じものが入っているんだから memo[i][j] == b[i, j] でしょ? |
 | その通り。じゃあ memo[i][j] はどんな規則性で並んでいる? |
 | b[i, j] と同じ漸化式が成り立つんでしょ?つまりこう。 |
memo[i][0] = memo[i - 1][0] + r[i - 1]
memo[0][j] = 0
memo[i][j] = min(memo[i - 1][j] + r[i - 1], memo[i - 1][j - 1] + f[i - 1]) (j > 0)
 | これを再帰を使わずに求められるかしら。 |
 | memo[i][0], memo[0][j] = 0 はすぐできる。memo[i][j] は、ええと。 |
 | roadTime = {1, 2, 6}, flightTime = {4, 3, 5}, K = 2 の場合をもう一度考えましょうか。 |
 | まず memo[0][j] = 0 だから memo[0][0] = 0, memo[0][1] = 0, memo[0][2] = 0 だね。それから memo[i][0] = memo[i - 1][0] + r[i]。残りの memo[i][j] も全部計算して表にするとこんな感じ。 |
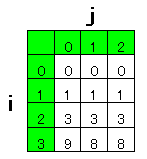
 | じゃあプログラムにしてみましょうか。動的計画法は英語で Dynamic Programming というので配列の名前は dp にすることが多いみたいよ。 |
 | 書けた。 |
public int minTime(int N, int[] roadTime, int[] flightTime, int K) {
int dp[][] = new int[N + 1][K + 1];
for (int j = 0; j <= K; j++)
dp[0][j] = 0;
int road;
for (int i = 1; i <= N; i++) {
for (int j = 0; j <= K; j++) {
road = dp[i - 1][j] + roadTime[i - 1];
if (j > 0)
dp[i][j] = Math.min(road,
dp[i - 1][j - 1] + flightTime[i - 1]);
else
dp[i][j] = road;
}
}
return dp[N][K];
}
 | これなら明らかに O(NK) よね。 |
 | System test 通った。ようやく終わりだ。長かった。 |
 | 結構がんばったわね。あんたにしては。 |
 | ああ、自分をほめてあげたいよ。。。 |
 | あと、最初の全探索の例はもしかして要らなかった? |
 | 初心者の場合は「全探索で問題を把握」 -> 「漸化式を作る」 -> 「再帰を書く」 -> 「動的計画法を書く」の順にやると混乱が少なくて済むからよ。いきなり漸化式から始めてたらこなたは挫折してたでしょ。 |
 | うん。。。 |
 | ところで今回はテーマが動的計画法なので言わなかったけど、以下のコードでも解けるわ。 |
public int minTime(int N, int[] roadTime, int[] flightTime, int K) {
int[] delta = new int[roadTime.length];
int total = 0;
for (int i = 0; i < roadTime.length; i++) {
delta[i] = roadTime[i] - flightTime[i];
total += roadTime[i];
}
Arrays.sort(delta);
for (int i = delta.length - 1; i >=0 && K > 0 && delta[i] > 0;
i--) {
total -= delta[i];
K--;
}
return total;
}
 | そうか。陸路と空路の差が大きいものから順に選べば良いのか。動的計画法が無くても解けるじゃん。なんで黒井先生はこの問題を選んだんだろう。 |
 | 動的計画法が必須の問題だとそれなりに難しい問題になっちゃうから入門用ってことでこれにしたんじゃない? |
 | つまりスラ○ムを倒すためにイオ○ズンを使ったってこと?やれやれ、どうせならアークデー○ンあたりの手ごたえのある問題が欲しかったよ。 |
 | (コ、コイツ終わったのをいいことに心にも無いことを。。。) |
 | よう言うた!お前がそんなに勉学に興味を持つようになるとは!教師生活 25 年!こんな嬉しい事は無いでー! |
 | い、いや、あのそういうわけでは。あと先生は 27 歳では。。。 |
 | そんなお前にプレゼントや! |
王様は長い間出張していたので、できるだけ早く女王のもとに帰りたいと思っています。王様は都市 0 におり、女王は都市 N (1 <= N <= 400000)に居ます。全ての都市 i (0 <= i <= N - 1) に対して陸路と空路があります。配列 roadTime, flightTime が与えられ、それぞれの i 番目の要素は都市 i から都市 i + 1 までの陸路、空路の所要時間 (1 以上 100000 以下) を表わします。roadTime は以下の式で生成されます。
roadTime[0] = roadFirst mod roadMod;
for i = 1 to N-1
roadTime[i] = (roadTime[i-1]*roadProd + roadAdd) mod roadMod;
flightTime は flightFirst, flightProd, flightAdd, flightMod を使って同じように生成されます。しかし王国の科学力は低く、空路による移動は離陸に失敗する危険を伴います。そのため、王女は王様に空路は K (0 <= K <= 40 かつ 0 <= K <= N) 回までに留めるように言いました。危険なのは離陸のみなので、複数の都市を連続して空路で移動する場合は一回と数えます。王様が王女に会うための最短時間を求めなさい。
出題元 SRM 468 Div1 500
 | い、いえ結構です。 |
 | そうか!嬉しいか!ワイも嬉しいでー!ほながんばりやー。 |
 | い、行ってしまった。。。か、かがみん、あの。。。 |
 | 自業自得ね。私は帰るから自力で頑張りなさい。 |
 | そ、そんな。待っ。。。本当に帰っちゃった。くそー。帰ってアニメを観なければいけないというのに! |
 | ラスボスを倒したと思ったらそれは全部夢で2周目がようやく本番だったような気分だ。しかも2周目は格段に難しいし。 |
 | とりあえずやってみるか。落ち着け、落ち着くんだ。素数を数えて落ち着くんだッ。。。 |
 | よく見るとさっきの問題を難しくしただけみたいだ。 |
 | まずは問題を理解するために全探索の例を書いてみるか。 |
 | 陸路と空路の列を全部求めておいて、それに対して全探索と。 |
 | さっきと違う点は、連続した空路は一つにまとめられるということ。だから、直前が空路かどうかを prevIsFlight というフラグで表わして書けば良いか。 |
 | はあ、フラグという言葉はギャルゲだけで使いたかったなあ。 |
 | とりあえず書いてみた。 |
private int[] roadTime, flightTime;
public long minTime(int N, int roadFirst, int roadProd, int roadAdd, int roadMod,
int flightFirst, int flightProd, int flightAdd, int flightMod, int K) {
roadTime = new int[N];
roadTime[0] = roadFirst % roadMod;
for (int i = 1; i < N; i++)
roadTime[i] = (int)(((long)roadTime[i - 1] * roadProd + roadAdd) % roadMod);
flightTime = new int[N];
flightTime[0] = flightFirst % flightMod;
for (int i = 1; i < N; i++)
flightTime[i] = (int)(((long)flightTime[i - 1] * flightProd + flightAdd) % flightMod);
long sum, min = Integer.MAX_VALUE, flight;
boolean prevIsFlight;
for (int i = 0; i < (1 << N); i++) {
sum = 0;
flight = 0;
prevIsFlight = false;
for (int j = 0; j < N; j++) {
if ((i & (1 << j)) != 0) {
if (!prevIsFlight) {
flight++;
prevIsFlight = true;
}
sum += flightTime[j];
} else {
sum += roadTime[j];
prevIsFlight = false;
}
}
if (flight <= K && min > sum)
min = sum;
}
return min;
}
 | お、サンプル通った。でもやっぱ System test は TLE か。 N=400000じゃ絶対無理だよなあ。まあ、問題文の理解は合っていることがわかったので次に行こう。 |
 | まーだやってんの。 |
 | あ!かがみん!口では帰ると言っておきながら気になって見に来てくれるなんて!あんたツンデレの鑑だよ。。。 |
 | 相変わらず目線がおかしいわね。で、どこまで行ったのよ。 |
 | 全探索まで書いた。。。 |
 | 次は漸化式ね。私もこの問題初見だから考えながらやるわ。 |
 | ってかがみん、お菓子食べ過ぎなんじゃ。。。 |
 | いいのよ放課後なんだし。で、漸化式は。 |
 | 直前が空路かどうかを条件に入れないといけない。 |
 | そうねえ。状態を増やしたくないけどとりあえず入れてみようか。 b[i, j, true|false] の形ね。 |
 | b[0, j, false] = 0, b[0, j, true] = 0 まではわかる。 |
 | まあ、出発地に居るだけだからな。 b[i, j, false] を考えなさいよ。 |
 | うぐ。ええとお。直前が空路じゃないから b[i, j, false] = min(b[i - 1, j, true] + roadTime[i - 1], b[i - 1, j, false] + roadTime[i - 1]) |
 | b[i, j, true] は直前が空路だから j > 0 の場合はずっと空路なのか、直前から空路なのかで比較が必要ね。
よって b[i, j, true] = min(b[i - 1, j - 1, false] + flightTime[i - 1], b[i - 1, j, true] + flightTime[i - 1]) |
 | あと j = 0 の場合は b[i - 1, j, true] + flightTime[i - 1] だね。 |
 | それから最終状態は、 b[N, K, false] の b[N, K, true] のどちらか小さい方を選ばなきゃいけないってもの忘れずにね。じゃあ書いてみて。 |
private int[] roadTime, flightTime;
public long minTime(int N, int roadFirst, int roadProd, int roadAdd, int roadMod,
int flightFirst, int flightProd, int flightAdd, int flightMod, int K) {
roadTime = new int[N];
roadTime[0] = roadFirst % roadMod;
for (int i = 1; i < N; i++)
roadTime[i] = (int)(((long)roadTime[i - 1] * roadProd + roadAdd) % roadMod);
flightTime = new int[N];
flightTime[0] = flightFirst % flightMod;
for (int i = 1; i < N; i++)
flightTime[i] = (int)(((long)flightTime[i - 1] * flightProd + flightAdd) % flightMod);
return Math.min(b(N, K, false), b(N, K, true));
}
private long b(int i, int j, boolean prevIsFlight) {
if (i == 0)
return 0;
if (prevIsFlight) {
if (j > 0) {
return Math.min(
b(i - 1, j - 1, false) + flightTime[i - 1],
b(i - 1, j, true) + flightTime[i - 1]);
} else {
return b(i - 1, j, true) + flightTime[i - 1];
}
} else {
return Math.min(b(i - 1, j, true) + roadTime[i - 1],
b(i - 1, j, false) + roadTime[i - 1]);
}
}
 | あれ?サンプルが通らない。そうか。初めて選ぶ場合には、前回が空路ってことはありえないから b[0, j, true] = 0 ではなく b[0, j, true] = [ありえない] だね。ありえないってどうやって表現するんだろ。 |
 | 候補として選択されないようにするってことだから充分大きい値を入れれば良いわね。 N が 400000 以下で roadMod, flightMod が 100000 以下だから最大でも 4 * 10^10 ね。だから Long.MAX_VALUE / 2 を入れておけば充分よ。 |
 | 何で 2 で割るの? |
 | Long.MAX_VALUE に 1 を足すと負の値になっちゃうからよ。 |
private int[] roadTime, flightTime;
public long minTime(int N, int roadFirst, int roadProd, int roadAdd, int roadMod,
int flightFirst, int flightProd, int flightAdd, int flightMod, int K) {
roadTime = new int[N];
roadTime[0] = roadFirst % roadMod;
for (int i = 1; i < N; i++)
roadTime[i] = (int)(((long)roadTime[i - 1] * roadProd + roadAdd) % roadMod);
flightTime = new int[N];
flightTime[0] = flightFirst % flightMod;
for (int i = 1; i < N; i++)
flightTime[i] = (int)(((long)flightTime[i - 1] * flightProd + flightAdd) % flightMod);
return Math.min(b(N, K, false), b(N, K, true));
}
private long b(int i, int j, boolean prevIsFlight) {
if (i == 0)
return prevIsFlight ? Long.MAX_VALUE / 2 : 0;
if (prevIsFlight) {
if (j > 0) {
return Math.min(
b(i - 1, j - 1, false) + flightTime[i - 1],
b(i - 1, j, true) + flightTime[i - 1]);
} else {
return b(i - 1, j, true) + flightTime[i - 1];
}
} else {
return Math.min(b(i - 1, j, true) + roadTime[i - 1],
b(i - 1, j, false) + roadTime[i - 1]);
}
}
 | やっとサンプル通った。。。 |
 | コレ大変ね。。。 |
 | うん。。。これでもまだ TLE するしね。。。 |
 | (ガラガラ)はッ! |
 | あっ。 |
 | こ、これは!すいません!すいません!夕暮れの教室で二人っきりで超絶百合展開いえ仲むつまじくされているところをお邪魔するなんて! |
 | ち、違、これは。 |
 | こ、この件は私の心の中に留めておいて誰にも言いません!ただ新作のネタにはします! |
 | いや、そーゆんじゃないんだって。 |
 | で、できればそのまま続けて下さい。私はお邪魔にならないように見守らせていただきます。 |
 | だ、だから違うんだよー。 |
 | え。誤解?うおー!また私ってば先輩をネタに腐った妄想をー! |
 | しかし!これが私!これぞ生きている証!創作意欲が湧いて来た!早速帰ってネームにします! |
 | い、行っちゃった。 |
 | あの子あんたにそっくりね。 |
 | ぐは!反論したいが!反論できないッ! |
 | 今日はもう疲れたから続きは明日にしましょう。 |
~翌日~
 | うう。。。 |
 | どうしたの? |
 | 夢の中に動的計画法が出てきてずっとうなされてた。 |
 | 私もよ。。。何なのかしらね。コレ。 |
 | ぷよぷよやった後にぷよぷよの夢を見るのと同じかな。 |
 | まあ似たような感覚ね。 |
 | ギャルゲやった後に仮想と現実の区別がつかなくなるのも同じかな。 |
 | それはあんただけよ!昨日の再帰を動的計画法に書き直すわよ。 |
 | 意外に簡単に書き直せた。 |
public long minTime(int N, int roadFirst, int roadProd, int roadAdd, int roadMod,
int flightFirst, int flightProd, int flightAdd, int flightMod, int K) {
int[] roadTime = new int[N];
roadTime[0] = roadFirst % roadMod;
for (int i = 1; i < N; i++)
roadTime[i] = (int)(((long)roadTime[i - 1] * roadProd + roadAdd) % roadMod);
int[] flightTime = new int[N];
flightTime[0] = flightFirst % flightMod;
for (int i = 1; i < N; i++)
flightTime[i] = (int)(((long)flightTime[i - 1] * flightProd + flightAdd) % flightMod);
long dp[][][] = new long[N + 1][K + 1][2];
for (int j = 0; j <= K; j++) {
dp[0][j][0] = 0;
dp[0][j][1] = Long.MAX_VALUE / 2;
}
long flight;
for (int i = 1; i <= N; i++) {
for (int j = 0; j <= K; j++) {
flight = dp[i - 1][j][1] + flightTime[i - 1];
if (j > 0)
dp[i][j][1] = Math.min(
dp[i - 1][j - 1][0] + flightTime[i - 1], flight);
else
dp[i][j][1] = flight;
dp[i][j][0] = Math.min(
dp[i - 1][j][1] + roadTime[i - 1],
dp[i - 1][j][0] + roadTime[i - 1]);
}
}
return Math.min(dp[N][K][0], dp[N][K][1]);
}
 | サンプル通ったけど System test は java.lang.OutOfMemoryError: Java heap space が出るね。動的計画法にしたのに。 |
 | N = 400000, K = 40 のケースだとメモリが足りないわね。 |
 | roadTime と flightTime は配列で持っておく必要無いんじゃないの? |
 | 確かにそうだけどそこを削っても焼け石に水よ。 dp[ ][ ][ ] を何とかしないと。 |
 | N の 400000 は多いよね。 |
 | 漸化式を見ると、直前の i の配列しか使っていないから i に関しては 2 つだけ用意すれば良いわね。これでメモリサイズのオーダーを O(NK) から O(K) に減らせるわ。 |
public long minTime(int N, int roadFirst, int roadProd, int roadAdd, int roadMod,
int flightFirst, int flightProd, int flightAdd, int flightMod, int K) {
int[] roadTime = new int[N];
roadTime[0] = roadFirst % roadMod;
for (int i = 1; i < N; i++)
roadTime[i] = (int)(((long)roadTime[i - 1] * roadProd + roadAdd) % roadMod);
int[] flightTime = new int[N];
flightTime[0] = flightFirst % flightMod;
for (int i = 1; i < N; i++)
flightTime[i] = (int)(((long)flightTime[i - 1] * flightProd + flightAdd) % flightMod);
long dp[][][] = new long[2][K + 1][2];
for (int j = 0; j <= K; j++) {
dp[0][j][0] = 0;
dp[0][j][1] = Long.MAX_VALUE / 2;
}
long flight;
for (int i = 1; i <= N; i++) {
for (int j = 0; j <= K; j++) {
flight = dp[(i - 1) & 1][j][1] + flightTime[i - 1];
if (j > 0)
dp[i & 1][j][1] = Math.min(
dp[(i - 1) & 1][j - 1][0] + flightTime[i - 1],
flight);
else
dp[i & 1][j][1] = flight;
dp[i & 1][j][0] = Math.min(
dp[(i - 1) & 1][j][1] + roadTime[i - 1],
dp[(i - 1) & 1][j][0] + roadTime[i - 1]);
}
}
return Math.min(dp[N & 1][K][0], dp[N & 1][K][1]);
}
 | (i & 1) って何? |
 | 数字の下位 1 bit を取り出しているの。つまり奇数なら 1 偶数なら 0 を返すようして、これを使って配列を切り替えているのよ。 |
 | なるほど。 |
 | よし! System test 通った! |
 | せっかくだから roadTime と flightTime の配列を消してみる。 |
public long minTime(int N, int roadFirst, int roadProd, int roadAdd, int roadMod,
int flightFirst, int flightProd, int flightAdd, int flightMod, int K) {
long dp[][][] = new long[2][K + 1][2];
for (int j = 0; j <= K; j++) {
dp[0][j][0] = 0;
dp[0][j][1] = Long.MAX_VALUE / 2;
}
long roadTime = roadFirst % roadMod;
long flightTime = flightFirst % flightMod;
long flight;
for (int i = 1; i <= N; i++) {
for (int j = 0; j <= K; j++) {
flight = dp[(i - 1) & 1][j][1] + flightTime;
if (j > 0)
dp[i & 1][j][1] = Math.min(
dp[(i - 1) & 1][j - 1][0] + flightTime, flight);
else
dp[i & 1][j][1] = flight;
dp[i & 1][j][0] = Math.min(
dp[(i - 1) & 1][j][1] + roadTime,
dp[(i - 1) & 1][j][0] + roadTime);
}
roadTime = (roadTime * roadProd + roadAdd) % roadMod;
flightTime = (flightTime * flightProd + flightAdd) % flightMod;
}
return Math.min(dp[N & 1][K][0], dp[N & 1][K][1]);
}
 | System test 通った! |
 | ようやくこれで終わりね。 |
 | 。。。 |
 | あら静かね。 |
 | また黒井先生が現れないように黙っている。 |
 | お。終わったらしいなー。ようやったようやった。 |
 | い、いつの間に背後に。 |
 | じゃあ次の問題行くで。 |
 | 「こなたはにげだした!」 |
 | 「しかしまわりこまれてしまった!」 |
こちらのらき☆すたアイコンを使わせていただきました
参考文献: iwi さんの資料



































































































































































































