確率解説 [SRM 418 Div2 500/Div1 250]

問題

昨日、くじの広告を見掛けた。「 m 個の数字を選んでください。その後で我々もランダムに m 個の数字を選びます。少なくとも k 個の数字が一致していればあなたの勝ち！」あなたが勝つ確率を求めよ。
ただし $2 ≦ n ≦ 8, 1 ≦ m ≦ n - 1, 1 ≦ k ≦ m$ とする。

解答

	えっと、どっから手をつけたら良いかわからないよ。。。
	TopCoder の問題はひねってあるからね。こういうときは簡単な問題に分解してみましょう。まずはこの問題。

Q1) n 個の中に 1 個の当たりがある場合、 1 個引いて当たりである確率を求めよ。

	さすがにこれは分かるよ。 $\frac{1}{n}$ でしょ？
	ふむ、では次の問題。

Q2) n 個の中に m 個の当たりがある場合、 1 個引いて当たりである確率を求めよ。

	ぐっと難しくなったね。。。
	ここでつまずくということは Q1 をきちんと理解していないということね。
	えー、そうなの？。
	もう一度 Q1 に戻りましょう。確率の問題の基本は「場合の数」よ。「事象が起こる場合の数」/「全体の場合の数」で求めるの。
	うん
	まず「事象が起こる場合の数」というのは、「当たりを引く場合の数」ということね。
	うん
	つまり「 1 個の当たりの中から 1 個を取り出す場合の数」ということなの。
	何か回りくどいね。結局 ${}_{1}C_{1} = 1$ ってことでしょ？
	そうね。今は回りくどいと思うだろうけど、後で役に立つから。次は「全体の場合の数」ね。これは「n 個の中から 1 個を取り出す場合の数」なので ${}_{n}C_{1}$ 。よって確率は $\frac{{}_{1}C_{1}}{{}_{n}C_{1}} = \frac{1}{n}$ 。
	そこまでは大丈夫。
	これをもとに Q2 を考えるの。まず「事象が起こる場合の数」は？
	「当たりを引く場合の数」っていう言葉は Q1 と同じだけど、今回は当たりが m 個あるよね。こういう場合はいくつになるんだろう。
	m 個ある当たりくじの中から 1 個を取り出すと考えたら？
	${}_{m}C_{1}$ ？
	そういうことね。
	ちょ、ちょっと待って。 Q1 の場合はどうなんだっけ。
	1 個しかないものから 1 個取り出すから ${}_{1}C_{1}$ 。
	そっかー Q1 はそれで 1 なんだー。今やっと Q1 が分かった気がする。
	次に「全体の場合の数」は？
	n 個の中から 1 個を取るというのは Q1 と変わらないから Q1 と同じで ${}_{n}C_{1}$ かな？
	そうよ。なので Q2 の答えは $\frac{{}_{m}C_{1}}{{}_{n}C_{1}} = \frac{m}{n}$ 。
	ぷはー。なかなか大変。あとどれくらい？
	まだ一割ぐらいよ。。。
	う、うそ。。。ちょっとお菓子食べて休憩したいなー、なんて。。。
	しょうがないわね。休憩終わったら Q3 を始めるわよ。

Q3) n 個の中に m 個の当たりがある場合、 m 個引いて全て当たりである確率を求めよ。

	「事象が起こる場合の数」＝「m 個引いて全て当たりの場合の数」だけど、これはいくつになるんだろう。
	m 個の当たりの中から m 個を取り出すことになるわね。
	そうすると ${}_{m}C_{m}$ ？
	そう
	「全体の場合の数」は、「 n 個の中から m 個を取り出す場合の数」だから ${}_{n}C_{m}$ ？
	そう
	じゃあ答えは $\frac{{}_{m}C_{m}}{{}_{n}C_{m}} = \frac{1}{{}_{n}C_{m}}$ だー。何かコツがわかった気がするー。
	ふむ、いいわね。次。

Q4) n 個の中に m 個の当たりがある場合、 m 個引いて 1 個が当たりである確率を求めよ。

	ここが一番の山場よ。
	じゃあ、私は隣でお菓子を食べながら二人を眺めるとするよ。
	急に出てきたわね。邪魔しないでよね。。。
	あー、続けて続けて。私はかがみんの新しい魅力を堪能しに来ただけだから。伊達メガネ掛けて差し棒を持ってタイトスカートにワイシャツを着てもらえば言う事無いんだけどねー。
	あ、胸のボタンは第二まで開けてね。
	帰れ。
	え、えーと「事象が起こる場合の数」から求めるんだよね？
	とりあえず外野は無視して続けましょう。。。
	これは今までのやり方で行くと、「事象が起こる場合の数」＝「m 個の当たりの中から 1 個を取り出す場合の数」 $= {}_{m}C_{1}$ 。
	多分そうやると思ったけど不正解ね。それだと n 個から 1 個を取り出す場合の数になっちゃうわ。今回は n 個から m 個取り出すのよ。そして取り出した m 個の中の 1 個が当たりなの。
	そっか。。。どうやって考えたらいいんだろ。。。
	n 個から 1 個の当たりと m - 1 個のはずれを同時に取り出すと考えたら？
	一瞬「なるほど！」って思ったけど式にはできません。。。
	分けて考えるの。まず当たりを取り出す場合の数は m 個の中から 1 個の当たりを取り出すから ${}_{m}C_{1}$ 。はずれは n - m 個で、この中から m - 1 個を選ぶので ${}_{n - m}C_{m - 1}$ 。
	「全体の場合の数」はわかるかも。 n 個から m 個取り出すから ${}_{n}C_{m}$ ？
	そうね。よって確率は $\frac{{}_{m}C_{1} \times {}_{n - m}C_{m - 1}}{{}_{n}C_{m}}$ になるわ。
	これで Q4 は終わりだね。
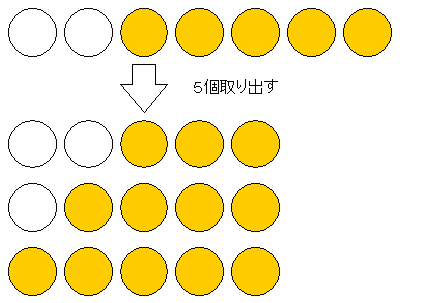
	でもこの問題には引っ掛けがあるの。n = 7, m = 5の場合はどうなる？
	さっきの式にそのまま当てはめると $\frac{{}_{5}C_{1} \times {}_{2}C_{4}}{{}_{7}C_{5}}$ になるけど分母の ${}_{2}C_{4}$ は変だね。 2 個の中から 4 個選ぶことになっちゃう。
	そうね。ちょっとさっき求めた数式を離れて考えると、n = 7, m = 5の場合っていうのは、 7 個のうち 5 個が当たりで、その中から 5 個を選ぶってことよね。
	うん
	下の図のように、選び方は３通りなんだけど、どの選び方をしても3 個以上 5 個以下の当たりが必ず含まれるの。だから Q4 のように 1 個選ばれる確率を求めようとすると 0 になっちゃうのよ。

	そっかー。
	これを一般化すると、 n 個から m 個取り出して、 m 個に含まれる最小の当たりの個数 > 1 なら確率は 0 になるわね。言い換えると m 個に最も多くはずれを含ませた場合の、 m 個内の当たりの個数 > 1 ということね。
	はずれの個数は n - m 個だから、 $m - (n - m) > 1$ つまり $2 m - n > 1$ なら確率は 0 になるわ。
	機械的にやるんじゃだめなんだねー。
	ここまでくれば、後はそんなに難しく無いわ。

Q5) n 個の中に m 個の当たりがある場合、 m 個引いて k 個当たりである確率を求めよ。

	さっきの Q4 の 1 の部分が k に変わっただけだね。 $2 m - n > k$ なら確率は 0。それ以外の場合は $\frac{{}_{m}C_{k} + {}_{n - m}C_{m - k}}{{}_{n}C_{m}}$ 。
	最後に当初の問題よ。

Q6) n 個の中に m 個の当たりがある場合、 m 個引いて k 個以上が当たりである確率を求めよ。

	Q5 で k の場合を求めてあるので、当たりが k 個の場合から m 個の場合まで足せば良いから $\frac{\sum_{i = k}^{m} a_{k}}{{}_{n}C_{m}}$ だね。ここで $a_{k} = {}_{m}C_{k} + {}_{n - m}C_{m - k}$ ただし $2 m - n > k$ なら $a_{k} = 0$ 。
	Java で書くとこんな感じね。


import java.util.*;
public class TwoLotteryGames {
	public double getHigherChanceGame(int n, int m, int k) {
		long total = 1;
		for (int i = k; i < m; i++) {
			if (i >= 2 * m - n)
				total += combination(m, i) * combination(n - m, m - i);
		}
		return (double)total / combination(n, m);
	}

	// nCr
	private long combination(int n, int r) {
		if (n == r)
			return 1;
		if (n < r)
			throw new RuntimeException(n + " < " + r);
		if (n - r < r)
			r = n - r;
		long up = 1;
		for (int i = 0; i < r; i++)
			up *= n - i;
		long down = 1;
		for (int i = 2; i <= r; i++)
			down *= i;
		return up / down;
	}
}

	Div2 500 なのに結構深いんだねー。
	ところでかがみんはこの回には参加したの？
	参加はしてないわ。練習部屋で解いただけ。
	結果は？
	System test failed...
	えっ、そうなの？
	そ、その後で修正してちゃんと通したもん。。。
	へー。自分が間違えたくせに偉そうに解説なんかしてくれちゃってんのかー。やれやれかがみんも偉くなったもんだよ。いやー、まったく度胸があると言うかずうずうしいと言うか身の程知らずというか分不相応というか
	あれ？かがみん何で工具を持ってるの。。。何か作るの。。。
	ああ、それは世に言う「バールのような物」ですわね☆
	ま、待って！かがみん落ち着い（ガス

補足

	うーんうーん、私は、問題サイズ見た瞬間全探査しちゃうなぁ 0から1<<mまでi,jそれぞれbitcountがmになるのだけ調べて、&演算してbitcountしてk個以上か調べて終わりだから、あそこまで数学的要素は要らないかなーって印象
	というコメントが届いているみたいです。あ、かがみさんが席をはずしておられますので、せんえつながら私が対応させていただきます。
	確かにその通りですね。 $n ≦ 8$ なので $O (2^{n})$ のアルゴリズムが適用可能なサイズです。ですのでこちらのコードでも System test を通すことができます。


import java.util.*;
public class TwoLotteryGames {
	public double getHigherChanceGame(int n, int m, int k) {
		int match = 0, total = 0;
		for (int i = 0; i < (1 << n); i++) {
			if (bitCount(i) == m) {
				total++;
				if (bitCount(i & ((1 << m) - 1)) >= k)
					match++;
			}
		}
		return (double)match / total;
	}

	private int bitCount(int val) {
		int ret = 0;
		for (int i = 0; i < 32; i++) {
			if ((val & (1 << i)) != 0) {
				ret++;
			}
		}
		return ret;
	}
}

ただこちらのコードですと

n ≦ 29

という条件の場合は TLE (*1) してしまいます。
条件に応じて適切なアルゴリズムを選択すべきという好例ですね。

(*1) TLE: 時間超過 (Time Limit Exceeded) の略。 TopCoder においては 2 秒以内にプログラムが終了しなければならない。

	あっ！かがみさんが戻ってきたわ！いけない！怒りに我を忘れている！早く逃げて下さい！
	えっ
	あなたは Challenge し過ぎる！もう光弾も蟲笛も効かない！
	わー、みょー（ガス

こちらのらき☆すたアイコンを使わせていただきました

戻る

確率解説 [SRM 418 Div2 500/Div1 250]

目次

解答